[220305] 3b1b chapter 9, Dot products and duality

*Dot products- 내적

dot product를 구한다는 것은 같은 좌표값으로 짝을 지어 모두 더하고 곱하는 것을 의미 (결과는 scalar)

 

두 벡터 v, w의 dot product를 살펴보자.

벡터 w를 원점에서 시작하고 벡터 v위를 지나게 투영(projection, 투사)시키면 투영된 w 벡터의 길이에 벡터 v길이를 곱하는 것을 v*w 내적이라고 한다. (만약 w 벡터 투사체가 v 벡터 방향과 반대일 경우 내적은 음수가 된다.)

이와 반대로 v벡터를 w에 투영시켜도 내적은 같은 값이 나온다.

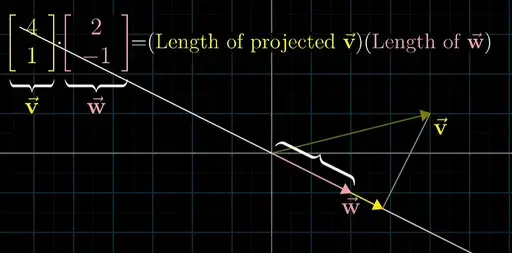
*즉 dot product, 내적은 순서가 중요하지 않다.

---

*이중성(duality)

각 행렬의 열들은 하나의 숫자로만 이루어진다.

1x2 행렬의 형태이다.

벡터 [4, 3]이 있다면 i-hat 4+ j-hat 3으로 생각하고 봐야 한다. 선형성에 따르면 같은 비율이어야 하기 때문에 i-hat 4 + j-hat 3과 같은 값이 된다. 즉

-2에 도착.

행렬-벡터의 곱이 두 벡터의 내적과 같다고 보인다.

임의 벡터 투영은 이 행렬에 임의 벡터를 곱하는 것이고, 이것은 계산적으로 u-hat과의 dot product와 같다.

즉 선형 변환 중 하나를 가지고 있다면, 어떻게 정의하든지 유일한 벡터가 그 변환에 대응된다.

벡터에서의 이중성이라는 것은, 그 벡터가 가진 선형변환 성질을 말한다. 1차원의 선형변환에서 이중이란, 공간상의 특정 벡터를 말한다.

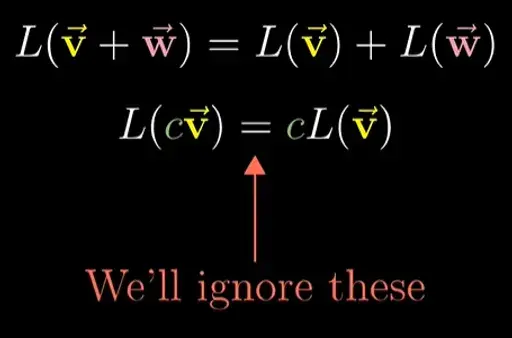
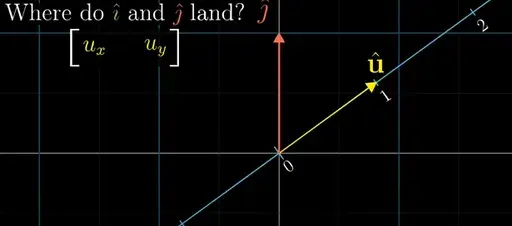
내적, dot product는

(1) 벡터가 같은 방향을 가르키는지 알아내고

(2) 두 벡터를 내적하는 것(dotting)은 두 벡터 중 하나를 변환인자로 보는 것

 

이다.